周末,是學習數學史的好時機! 🤓大石蝦皮商城:https://reurl.cc/Dg5age
畢達哥拉斯(Pythagoras)是最早的數學先驅之一,他在公元前571年出生於希臘的薩摩斯島(Samos),最後在義大利南部的克羅托內(Crotona)創辦了一個古怪的數學學派,他的門徒不許吃豆子、碰白羽毛,或在陽光下「撒尿」。他並沒有發明那個關於斜邊上正方形面積的著名定理(x² + y² =z²),而是給出了證明。(圖文摘自《費波納契的兔子:50個改變歷史的數學大觀念》)
💡網路書店:
博客來:https://reurl.cc/9r8Mrj
誠品線上:https://reurl.cc/ZGxDjA
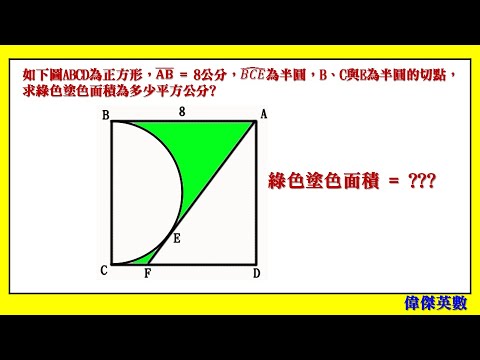
同時也有1部Youtube影片,追蹤數超過11萬的網紅GreatKidsLearning,也在其Youtube影片中提到,利用圓外一點到切點等距、畢氏定理、三角形面積、圓面積及正方形面積公式來解題 歡迎大家加入會員,贊助此影音頻道...
「正方形面積」的推薦目錄:
- 關於正方形面積 在 國家地理雜誌 Facebook 的精選貼文
- 關於正方形面積 在 余海峯 David . 物理喵 phycat Facebook 的精選貼文
- 關於正方形面積 在 我愛精品代購 Facebook 的精選貼文
- 關於正方形面積 在 GreatKidsLearning Youtube 的最佳貼文
- 關於正方形面積 在 [幾何] 1/4圓內接正方形面積- 看板Math 的評價
- 關於正方形面積 在 05 正方形的面積公式 - YouTube 的評價
- 關於正方形面積 在 06 正方形面積公式的應用 - YouTube 的評價
- 關於正方形面積 在 您可以向孩子解釋「正方形」和「長方形」的面積公式由來嗎? 的評價
- 關於正方形面積 在 29 1 正方形、长方形面积计算小學奧數四年級幾何 - YouTube 的評價
正方形面積 在 余海峯 David . 物理喵 phycat Facebook 的精選貼文
世上有無字的情批,也有無字的數學證明。光靠這張圖就可以證明的事情是:【根號二是無理數】 原解釋影片 by @Mathologer youtu.be/f1yDExNAEMg
以下導讀 😃:
我們想像北韓大閱兵,兩個一樣大的步兵方陣向彼此靠近,交錯穿過(像之前回顧的動畫),然後迅速的重新整隊,變成一個有兩倍軍人的方陣......啊,此情此景多賞心悅目,金正妹大喜。
呃,什麼,數學很好的參謀表示,很抱歉那是不可能做到的!如果小方陣邊長是 N,大方陣邊長是 M,因為士兵守恆
N² + N² = M²
→ 2 N² = M²
→ (M/N) = √2
但 M 和 N 都是正整數。就表示根號二忽然變有理數了,即使在已經頗無理的北韓都做不到那種事。
但怎麼證明?數一數,圖中有兩個淺色邊長為 12 的正方形,彼此在中央重疊 7 格深色正方形,12 - 7 = 5 是角落兩個白色正方形,整個大正方形邊長是 12 + 5 = 17。
注意到 12×12 = 144, 144 + 144 = 288 ≠ 289 = 17×17 只差 1 就可以完成北韓方陣,很好很好,只需要多複製出一個人(誤)。
能否更好,不需要偷加減一個人呢。依照前文,假設能完成 2 N² = M² 的最小正整數 M 與 N 存在,容易檢查
( 2N - M )² = 2 (M - N)² 也成立。
上式可以用代數乘開,或者注意到原圖中的正方形的面積關係。若兩個淺色正方形面積相加等於大正方形,則中央重疊正方形面積,會等於兩個角落的白色小正方形。(我想像它們是蛋糕模子裡的麵糊,抹平推開。)
揪抖嗎跌~發現貓溺。我們剛剛不是才假設 M,N 是最小的能滿足方程式的正整數解嗎。但透過代數 or 幾何推理,忽然又冒出一組「更小的正整數」 2N-M 和 M-N 也是解。
按照一樣的運算可以一再不停「找出」嚴格更小的正整數組.......
但正整數不可能一直減小再減小,最小只有到 1 而已。所以這一連串「無窮遞降」的荒謬劇的罪魁禍首,只有可能是我們一開始假設錯誤!並不存在任何這樣的 M,N。
這招「無窮遞降歸謬法」是由業餘數學家之王,律師先生費馬發揚光大的。→ Proof by infinite decent
值得一提的是,只要加減一個人就能完成北韓方陣。這個數學結論來自經典的 Pell 方程式:y² - 2 x² = ±1,這個 Pell 方程式的解可以輕易的得到越來越好的「√2 的有理近似」
例如
17/12 = 1.41666...
41/29 = 1.41379...
99/70 = 1.41428...
239/169 = 1.41420... (規律:p/q 的下一個是 (p+2q)/(p+q))
而 √2 = 1.41421...
欸欸欸為什麼?因為丟番圖 Diophantus 和婆羅摩笈多 Brahmagupta 強者威能,歐幾里得也有貢獻。詳盡展開字多略。
正方形面積 在 我愛精品代購 Facebook 的精選貼文
愛馬仕CP值超高的飾品收納盤🔥
這個雙色皮革盤功能超實用
讓你的桌子不再看起來凌亂了
還可以保護你的飾品不受傷
有時到家就是要通通脫掉 才舒服
讓你的飾品有個溫暖的床😄
正方形面積=25*25 cm
🔹橘+夜空藍 15800
🔹夜空藍+巧克力棕 15800
🔹馬賽克煙灰缸零錢盤17500
愛馬仕更多飾品請看⬇️
https://www.hermes.com/nl/en/women/fashion-jewelry/leather-jewelry/#%7C%7C
家居小用品⬇️
https://www.hermes.com/nl/en/home/objects/#%7C%7C
男性專區⬇️
https://www.hermes.com/nl/en/men/jewelry-and-fashion-jewelry/#%7C%7C
本店商品都是本人親自專櫃採購!
提供專櫃配件+購買證明,請安心購買🙏
正方形面積 在 05 正方形的面積公式 - YouTube 的美食出口停車場

06 正方形面積 公式的應用. 均一教育平台Junyi Academy•34K views. Shorts. Number drawing shorts video for kids. How to draw many pictures using ... ... <看更多>
正方形面積 在 06 正方形面積公式的應用 - YouTube 的美食出口停車場

06 正方形面積 公式的應用. 34K views · 7 years ago ...more. Try YouTube Kids. An app made just for kids. Open app · 均一教育平台Junyi Academy. ... <看更多>





正方形面積 在 [幾何] 1/4圓內接正方形面積- 看板Math 的美食出口停車場
https://www.youtube.com/watch?v=6OfWw_etYUU
求其內接正方形面積?
我看下面留言說,設正方形的對角線長=D
又因為正方形的對角線長總是邊長的根號2倍, 故正方形面積是(D^2)/2
然後又說:根據畢氏定理, (D/2)^2+D^2=r^2=1 得D^2=0.8
所以正方形面積是0.4
可是,這算法我怎麼看,怎麼怪 @@
難道正方形的對角線就一定垂直於X軸嗎?
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 1.160.33.94 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1664639140.A.27E.html
... <看更多>