分享好文,中學生要學電腦嗎?
作者:創新工場CTO、人工智慧工程院執行院長 王詠剛
文章来自半轻人微信公众号(ban-qing-ren)
………………………………
朋友的孩子高中剛畢業,已拿到美國頂尖大學(非電腦專業)的錄取通知。疫情影響,不知何時才能去學校報到。孩子想抓緊學習一下程式設計,為大學打好基礎。這孩子找我聊了一個多小時,從如何學程式設計,聊到非電腦專業和電腦專業的路徑差異,又聊到如何從不同角度認識電腦與程式設計。聊得比較寬泛,不知是否對這孩子有用。
回想我自己的高中時代:那時雖迷戀程式設計,卻完全沒有懂行的人指導。在我們那個四線城市的廠礦中學裡,開設電腦興趣課的老師知道的資訊還沒我多。我高一時跑到北京中關村逛街,卻完全沒意識到中國第一代頂尖程式師當時就在我身邊的低矮辦公樓裡寫代碼(這話說得並不準確,比如求伯君那年就主要是在珠海做開發),鼎鼎大名的UCDOS、WPS、CCED就出自他們之手……我在當時街邊的一家書店(位置似乎就在今天的鼎好大廈對面)買到了許多種印刷品質極低劣的電腦圖書。用今天的標準看,那就是一批盜版影印或未授權翻譯的國外圖書。可那批書竟成了我高中時代最寶貴的程式設計知識來源。
顯然,我在高中時根本就是野路子學電腦。現在後悔也沒用,當時我的眼界或能觸及的資源就那麼多。如果能穿越回30年前,我該對喜歡程式設計的自己說些什麼呢?這些年,我與世界上最好的一批程式師合作過,也參與過世界上最有價值的軟體系統研發——我所積累的一些粗淺經驗裡,有哪些可以分享給一個愛程式設計的中學生?
【問題1】中學生要不要學電腦?
當然要!
每個中學生都要學。只不過——建議大部分中學生使用“休閒模式”,小部分(不超過10%)中學生使用“探險模式”。
啊?兩個模式?那我該進入哪個模式?⟹請跳轉至【問題2】
【問題2】選哪個模式?
你癡迷電腦嗎?比如,你玩遊戲時會特別想知道這遊戲背後的代碼是如何編寫的嗎?再比如,就算老師家長不同意你學電腦,甚至當著你的面把電腦砸了,你也要堅持學電腦嗎?如果是,恭喜你進入“探險模式”⟹請跳轉至【問題200】
你對數學有興趣嗎?比如,你看到街邊建築的曲線,就會在腦子裡琢磨曲線對應的函數或方程嗎?每當手裡攥著幾粒骰子,你就會不由自主地計算概率嗎?如果是,歡迎進入“探險模式”⟹請跳轉至【問題200】;當然,如果有些猶豫,也可以先進入“休閒模式”⟹請跳轉至【問題100】
即便你對電腦和數學興趣不大,家長、老師還是強烈建議你學電腦嗎?就算你一百個沒時間一千個不願意,家長、老師還是會逼著你學電腦嗎?如果是,建議你主動進入“休閒模式”並向家長、老師彙報說“我已經按照前谷歌資深軟體工程師的專業建議在認真學程式設計了”⟹請跳轉至【問題100】
其他情況,一律進入“休閒模式”。⟹請跳轉至【問題100】
【問題100】休閒模式 | 主要學什麼?
“休閒模式”將電腦視為我們生活、工作中的必備工具,主要學習如何聰明、高效、優雅地使用計算設備。這裡說的計算設備,包括所有形式的電腦、手機、遊戲機、智慧家電以及未來一定會進入生活的自動駕駛汽車。
什麼什麼?你已經會用電腦、會玩手機、會打遊戲了?別著急,慢慢往下看。
【問題101】休閒模式 | 我會用搜尋引擎嗎?
我知道你會用百度搜習題答案。但,習題答案不是知識。你會用搜尋引擎來搜索和梳理知識嗎?請試著用電腦和你喜歡的搜尋引擎來解決如下兩個問題:
(1)圓周率𝜋的計算方法有多少種?每種不同的計算方法分別是由什麼人在什麼時代提出的?借助電腦,今天人們可以將圓周率𝜋計算到小數點後多少位?將圓周率𝜋計算到小數點這麼多位元,一次大概需要花掉多少度電?
(2)全球大約有多少個廁所?在發展程度不同的國家,分別有多少比例的人可以享用安裝了抽水馬桶的衛生廁所?為什麼比爾·蓋茨曾大力推動一個設計新型馬桶的研發專案?比爾·蓋茨的公益組織在這個專案上大約花費了多少資金,最終收到了多大的效果?
如果你沒法快速得到上述問題的全部答案,那就給自己設一個小目標:一個月內,學會用搜尋引擎系統地獲取、梳理一組知識點的全部技巧。
【問題102】休閒模式 | 接下來學什麼?
建議學好典型的工具軟體。比如,我知道你會用Office了,但用Office和用Office是很不一樣的。對生活、學習、工作來說,學好、學透一個工具軟體比鑽研程式設計技巧更實用。
你會用Excel來管理班級公益基金的預算和實際收支情況嗎?
你會用Excel做出過去20年裡全球大學排名的演變趨勢圖嗎?
你會用Word排版一篇中學生論文嗎?論文中的圖表和最後的參考文獻部分該如何排版?
你會用Word編排一份班級刊物,包含封面、扉頁、目錄、插圖頁、附錄、封底等部分,可以在列印後直接裝訂成冊嗎?
PowerPoint呢?你有沒有研究過蘋果公司發佈會上那些幻燈片的設計?當約伯斯(多年以前)或蒂姆·庫克站在幻燈片前的時候,他們的演講思路是如何與幻燈片完美結合的?
還有哦,別忘了學學如何為數碼照片做後期,如何用電腦或手機剪視頻,如何為剪輯好的視頻配字幕,如何將照片、音樂、視頻等素材結合起來,做出一段吸引人的快手/抖音短視頻。
最後,抽空玩玩那些設計精妙的遊戲吧,比如《紀念碑穀》、《塞爾達傳說:曠野之息》之類;同時,遠離那些滿屏廣告,或者一心騙你在遊戲裡充值花錢的垃圾。
【問題103】休閒模式 | 不學學知識嗎?
當然要學知識。下面每種實用的電腦知識都夠大家學一陣子了。
(1)色彩知識:你知道同一張數碼照片在不同品牌的手機螢幕上、不同的電腦螢幕上、不同的智慧電視上顯示時,為什麼經常有較大色差嗎?你知道有一些色彩只適合螢幕顯示,不適合列印輸出嗎?你知道軟體工具裡常用的RGB、HSL之類的色彩空間都是什麼意思嗎?如何在設計PowerPoint幻燈片時選擇一組和諧美觀的色彩?
(2)字體知識:你知道什麼是襯線字體,什麼是無襯線字體嗎?你知道網頁中常用的英文字體都有哪些嗎?你知道商務演講時最適用于幻燈片的英文字體有哪些嗎?你知道電腦和手機常用的黑體、宋體、仿宋體、楷體等中文字體分別適合哪些實際應用場合嗎?你會將不同字體混排成一個美觀的頁面嗎?
(3)網路知識:你知道5G是什麼嗎?你知道5G和4G在通信頻寬、通信距離上的具體區別嗎?你知道什麼是路由器,什麼是防火牆嗎?你知道如何配置路由器,如何配置防火牆嗎?微信或QQ聊天時,對方發的文字、語音或視頻是如何傳送到你的手機上的?
(4)應用知識:淘寶中搜索得到的商品資訊是從哪裡來的?商品是按什麼方式排序的?為什麼購物APP經常會推薦給你一些曾經買過、看過的商品?你知道如何為自己建立個人網站嗎?你知道如何管理微信公眾號嗎?
(5)安全知識:你知道網路上的釣魚攻擊是怎麼回事兒嗎?你知道什麼是電腦漏洞嗎?你知道駭客為什麼想把一大批受攻擊的電腦變成可以遠端操控的傀儡機嗎?你知道為什麼現在很多手機APP都要通過短信發送驗證碼嗎?如果驗證碼被壞人截獲,你會面臨哪些風險?
這裡只是舉例。實用的電腦知識還有很多。大家可以自己發掘。
【問題104】休閒模式 | 我需要學程式設計嗎?
可以學,但不是必須。即便學,也只需要根據自己的需要,學那些最能幫你解決現實問題的部分。
【問題105】休閒模式 | 我該學什麼程式設計語言?
在“休閒模式”裡,電腦就是工具,程式設計也是工具,夠用就好。學什麼程式設計語言,完全看你想要電腦幫你做什麼。
• 如果你想對資料處理有更多自主權,那不妨學學Python;
• 如果你想做簡單的交互演示程式,那就先把JavaScript學起來;
• 如果你想更好、更快地寫論文,那不妨學學LaTeX(什麼什麼,LaTeX不是程式設計語言?你太小看LaTeX了);
• 如果你想學做簡單的手機APP,那麼,Android手機就學Java,蘋果手機就學Swift好了;
• 如果你只想知道程式設計是怎麼回事,那……從Python或JavaScript開始就行。其實,跟五六歲的小朋友一起學學Scratch圖形程式設計也不錯。
【問題106】休閒模式 | 我需要學人工智慧嗎?
在“休閒模式”裡,最需要學的不是“人工智慧的實現原理”,而是“什麼是人工智慧”,以及“人工智慧能做什麼,不能做什麼”。
• 在手機上試一試,人工智慧做語音辨識時能做到什麼水準?哪些話容易識別,哪些話不容易識別?
• 打開機器翻譯軟體,試一試哪些資訊翻譯得好,哪些資訊翻譯得不好?
• 手機上的拍照軟體一般都有人臉識別功能。試一試人臉識別在什麼場景下做得好,什麼場景下做得不好?
• 找一部講人工智慧的科幻電影,用自己的判斷解讀一下,電影裡哪些技術有可能成為現實,哪些技術存在邏輯矛盾。
【問題107】休閒模式 | 推薦什麼參考書、參考文獻?
書不重要,豆瓣評分7分以上的電腦應用、程式設計甚至科普類圖書都可以拿來翻翻。
直接在知乎裡搜索你想瞭解或學習的知識點可能更有效率。
如果你意猶未盡,覺得自己剛活動開筋骨,還想挑戰更高層次,歡迎進入“探險模式”。⟹請跳轉至【問題200】
否則,“休閒模式”到此結束。⟹請離開此問答
【問題200】探險模式 | 主要學什麼?
“探險模式”需要有挑戰精神。電腦科學的世界技術演進快,脈絡複雜,要想在探索時不迷路,你得通過有順序、有系統地學習電腦知識,慢慢構建出一張可以在未來幫你走得更遠的思維地圖來。
在“探險模式”裡,電腦就不止是一件能快速計算的工具了。電腦更像是我們大腦的一種延伸。這既包括認知能力的延伸,也包括認知邏輯的延伸。隨著學習深入,大家會逐漸體會到電腦所具有的多維度能力:
電腦是一種可以表示不同類型資訊(數、符號、文字、語音、圖像、視頻、虛擬空間、抽象邏輯)的“資訊管理機”;
同時,電腦也是一種可以連續執行指令以完成特定的資訊處理任務的“指令處理機”;
同時,電腦還是一種可以在知識與邏輯層面完成特定推理任務的“知識推理機”;
同時,電腦也是一種可以從人類給定的資料或自我生成的資料中總結規律,建立模型,自主完成某些決策的“智慧學習機”。
“探險模式”的目標就是盡可能準確地認識電腦,掌握有關電腦運行的最基本規律。有了這些基礎。未來在大學期間或工作中,你就能更容易地設計電腦軟硬體系統,或是設計出碳基大腦(人類)與矽基大腦(機器智慧)之間的最佳協作方案。
【問題201】探險模式 | 我的英語水準足夠嗎?
蘋果每年秋季的新品發佈會,不加字幕的話,你能聽懂多少?
能聽懂大部分:建議在學習電腦的過程中,盡可能使用英文教材、英文文檔。
能聽懂小部分:建議將原來準備學電腦的時間,分出一部分來學英語。
只能聽懂“你好”“再見”之類:⟹請離開此問答。然後,把原來準備學電腦的時間用於學英語,六個月後再回來。
【問題202】探險模式 | 我的數學水準足夠嗎?
如果你是數學和數學應用小能手——較複雜的數學問題總能快速找到核心思路,或快速簡化為簡單問題;很容易就能將抽象概念映射到具體的數學圖形,或將數學問題與相應的現實問題關聯在一起:請繼續探險之旅。
如果你應付正常數學課程感到吃力:建議將原來準備學電腦的時間,分出一部分來學數學。
如果你還搞不清楚什麼是方程、函數、集合、概率……:⟹請離開此問答。然後,把原來準備學電腦的時間用於學數學,六個月後再回來。
【問題203】探險模式 | 為什麼強調英語和數學?
(1)統計上說,最好的電腦參考資料大都是英文寫的,最好的電腦課程大都是用英文講的,最新的電腦論文大都是用英文發表的。
(2)函數、方程、坐標系、標量、向量、排列組合、概率這些中學數學裡會初步學習到的數學知識,是電腦科學的基礎。
【問題204】探險模式 | 電腦知識那麼多,正確的學習順序是什麼?
最重要的順序有兩個。建議先從順序一開始,學有餘力時兼顧兩個順序。
順序一:自底向上,即,自底層原理向上層應用拓展的順序。
電腦原理的基礎知識:
為什麼每台電腦(包括手機)都有CPU、記憶體和外部設備?
(馮·諾依曼體系結構的)記憶體中為什麼既可以存儲資料,也可以存儲指令?
CPU是如何完成一次加法運算的?
程式設計語言的基礎知識:
資料類型,值,變數,作用域……
語句,流程控制語句……
過程、方法或函數,類,模組,程式,服務……
編譯系統的基本概念:
電腦程式是如何被解釋或編譯成目標代碼的?
演算法和資料結構的基礎知識:
陣列,向量,鏈表,堆,棧,二叉樹,樹和圖……
遞迴演算法,排序演算法,二叉樹搜索演算法,圖搜索演算法……
應用層的基礎知識:
為什麼電腦需要作業系統?設備驅動程式是做什麼的?
網路通信的基本原理是什麼?流覽器是怎麼找到並顯示一個網頁的?
資料庫是做什麼用的?
虛擬機器是怎麼回事?
人工智慧系統的基礎知識:
先熟悉些線性代數、概率和數學優化的基礎知識。
什麼是機器學習?從簡單的線性回歸中體會機器學習的基本概念、基本思路。
什麼是神經網路?什麼是深度神經網路?為什麼神經網路可以完成機器學習任務?
如何使用PyTorch或TensorFlow實現簡單的深度學習功能?
順序二:自頂向下,即,自頂層抽象邏輯向下層具體邏輯拓展的順序。
• 電腦的本質是什麼?
• 什麼是圖靈機?什麼是通用圖靈機?
• 什麼是讀取﹣求值﹣輸出迴圈(Read–eval–print Loop,REPL)?
如何用自頂向下的方式理解(解析、解釋、編譯)一段程式碼?
• 靜態語言和動態語言的區別?
如何理解變數與資料類型之間的綁定關係?
• 什麼是函數式程式設計?
程式設計語言中,函數的本質是什麼?
函數為什麼可以像一個值一樣被表示、存儲、傳遞和處理?
• 什麼是物件導向?
類的本質是什麼?
如何用物件導向的方式定義個功能介面?
如何依據介面實現具體功能?
• 什麼是事件驅動?
什麼是事件?事件如何分發到接收者?
如何在事件驅動的環境中理解代碼的狀態和執行順序?
【問題205】探險模式 | 如何提高程式設計水準?
在掌握基本知識體系的基礎上,學好程式設計只有一條路:多程式設計,多參加程式設計比賽,多做程式設計題,多做實驗項目,多找實習機會——其中,能參與真實專案是最有價值的。
【問題206】探險模式 | 該從哪一門程式設計語言學起?
我個人推薦的程式設計入門語言(可根據情況任選):
Python
Java
Swift
C#
JavaScript / TypeScript
Ruby
……
可能不適合入門,但適合後續深入學習的語言:
C
C++
Go
Objective-C
組合語言
機器語言(CPU指令集)
Shell Script
Lua
Haskell
OCaml
R
Julia
Erlang
MATLAB
……
【問題207】探險模式 | 如何選參考書和參考資料?
(1)強烈推薦的參考書和參考資料:
• MIT、Stanford、CMU、UC Berkeley這四所大學中任何一個電腦專業方向使用的教學參考書或參考資料。網上可以查到這些學校電腦專業方向的課程體系,有的學校甚至公開了課程視頻。其中往往會列舉參考書和參考資料連結。
• 維琪百科(英文)上的數學、電腦科學相關條目。
• Github上star數在1000以上的開原始程式碼和開來源文件。
(2)強烈推薦但須小心辨別的參考資料:
知乎上的數學、電腦科學相關條目。使用時需要格外注意三件事:
儘量只看高贊答案或高贊文章;
辨別並避開廣告軟文;
辨別並避開純抖機靈的故事或段子。
Stack Overflow上的程式設計問題解答:
自己動手實驗,辨別解答是否有效。
CSDN上的程式設計問題解答:
自己動手實驗,辨別解答是否有效。
(3)其他推薦的參考書和參考資料:
國內專業作者寫作的專業技術書籍(豆瓣評分7分以上的)。
大廠(Google、Facebook、Microsoft、Amazon、阿裡、騰訊、百度、頭條等)資深工程師的技術公號、專欄、博客等。
著名圖書系列:如O’Reilly的動物封面的系列圖書(請注意最新版本和時效性)。
國內翻譯的著名技術圖書(譯本在豆瓣評分7分以上的)。
(4)儘量避免的參考書和參考資料:
• 已經過時的圖書或參考資料。
• 作者或譯者人數比章節數還多的專業圖書。
• 百度百科上的數學或電腦科學相關資料。
什麼什麼?你這篇問答居然沒有推薦一本具體的圖書?是,沒錯。如果你覺得即便有了上面的線索,自己還是找不到好書好資料,那也許你還是適合“休閒模式”⟹請跳轉至【問題100】
同時也有573部Youtube影片,追蹤數超過4萬的網紅吳老師教學部落格,也在其Youtube影片中提到,Python基礎程式語言應用證照班第10次上課 01_重點回顧與證照508最大公因數 02_證照508最大公因數解答 03_證照510費氏數列題目說明 04_證照510費氏數列無函式解答 05_證照510費氏數列加上函式解答 06_證照602撲克牌總和解答一 07_證照602撲克牌總和解答二改用串...
變數常數運算子 在 Taipei Ethereum Meetup Facebook 的最讚貼文
📜 [專欄新文章] 瞭解神秘的 ZK-STARKs
✍️ Kimi Wu
📥 歡迎投稿: https://medium.com/taipei-ethereum-meetup #徵技術分享文 #使用心得 #教學文 #medium
上一篇關於 zkSNARK扯到太多數學式,導致很難入手,這次介紹 STARK 會盡量減少數學式,以原理的方式跟大家介紹。
STARK 被視為新一代的 SNARK,除了速度較快之外,最重要的是有以下好處1. 不需要可信任的設置(trusted setup),以及
2. 抗量子攻擊
但 STARK 也沒這麼完美,STARK 的證明量(proof size)約 40–50KB,太佔空間,相較於 SNARK 只有288 bytes,明顯大上幾個級距。此外,這篇論文發佈約兩年的時間,就密碼學的領域來說,還需要時間的驗證。
STARK 的 S 除了簡潔(Succinct)也代表了擴展性(Scalable),而T代表了透明性(Transparency),擴展性很好理解,透明性指的是利用了公開透明的算法,可以不需要有可信任的設置來存放秘密參數。
SNARK 跟 STARK 都是基於多項式驗證的零知識技術。差別在於,如何隱藏資訊、如何簡潔地驗證跟如何達到非互動性。
快轉一下 SNARK 是如何運作的。
Alice 有多項式 P(x)、Bob有秘密 s,Alice 不知道 s、Bob 不知道 P(x)的狀況下,Bob 可以驗證P(s)。藉由同態隱藏(Homomorphic Hindings)隱藏Bob的 s → H(s),藉由 QAP/Pinocchio 達到了簡潔地驗證,然後把 H(s) 放到CRS(Common Reference String),解決了非互動性。細節可以參考之前的文章 。
問題轉換
零知識的第一步,需要先把「問題」轉成可以運算的多項式去做運算。這一小節,只會說明怎麼把問題轉成多項式,至於如何轉換的細節,不會多琢磨。
問題 → 限制條件 → 多項式
在 SNRAK 跟 STARK 都是藉由高維度的多項式來作驗證。也就是若多項式為: x³ + 3x² + 3 = 0,多項式解容易被破解猜出,若多項式為 x^2000000 + x^1999999 + … 則難度會高非常多。
第一步,先把想驗證的問題,轉換成多項式。
這邊以Collatz Conjecture為例子,什麼是Collatz Conjecture呢?(每次都用Fibonacci做為例子有點無聊 XD)
1. 若數字為偶數,則除以2
2. 若數字為奇數,則乘以3再加1 (3n+1)
任何正整數,經由上述兩個規則,最終結果會為 1 。(目前尚未被證明這個猜想一定成立,但也還未找出不成立的數字)
52 -> 26 -> 13 -> 40 -> 20 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1.
把每個運算過程的結果紀錄起來,這個叫做執行軌跡(Execution Trace),如上述52 -> 26 -> … -> 1。接著我們把執行軌跡轉換成多項式(由執行軌跡轉成多項式不是這裡的重點,這裡不會贅述,細節可以參考 StarkWare的文章 )如下
https://medium.com/starkware/arithmetization-i-15c046390862
合成多項式
接著就把這四個限制條件的多項式合成為一個,這個最終的多項式就叫做合成多項式(composition polynomial),而這個合成多項式就是後面要拿來驗證的多項式。
就像一開始提的,SNARK跟STARK都是使用高維度多項式,接著,來介紹STARK是藉由哪些方式,達到零知識的交換、透明性(Transparency)跟可擴展性(Scalability)。
修改多項式維度
這一步是為了後面驗證做準備的。在驗證過程使用了一個技巧,將多項式以2的次方一直遞減為常數項(D, D/2, D/4 … 1),大幅減低了驗證的複雜度。因此,需要先將多項式修改為2^n維度
假設上述的每個限制多項式(不是合成多項式喔)為Cj(x),維度為 Dj,D >= Dj 且 D 等於2^n,為了達到 D 維度,乘上一個維度(D -Dj)的多項式,
所以最終的合成多項式,如下
其中的αj、βj是由驗證者(verifier)所提供,所以最終的多項式是由證明方(prover)跟驗證方所共同組成。
*這小節的重點是將多項式修改成D維度,覺得多項式太煩可忽略
FRI
FRI 的全名是”Fast RS IOPP”(RS = “Reed-Solomon”, IOPP = “Interactive Oracle Proofs of Proximity”)。藉由FRI可以達到簡潔地驗證多項式。在介紹FRI 之前,先來討論要怎麼證明你知道多項式 f(x) 為何?
RS 糾刪碼:
糾刪碼的概念是把原本的資料作延伸,使得部分資料即可以做驗證與可容錯。其方式是將資料組成多項式,藉由驗證多項式來驗證資料是否正確。舉例來說,有d個點可以組成 d-1 維的多項式 y = f(x),藉由驗證 f(z1) ?= y,來確定 z1是否是正確資料。
回到上面的問題,怎麼證明知道多項式?最直接的方式就是直接帶入點求解。藉由糾刪碼的方式,假設有d+1個點,根據Lagrange插值法,可以得到一個 d 維的多項式 h(x),如果如果兩個多項式在(某個範圍內)任意 d 點上都相同( f(z) = h(z), z = z1, z2…zd),即可證明我知道 f(x)。但是我們面對的是高維度的多項式,d 是1、2百萬,這樣的測試太沒效率,且不可行。FRI 解決了這個問題,驗證次數由百萬次變成數十次。
降低複雜度
假設最終的合成多項式為 f(x),藉由將原本的1元多項式改成2元多項式,以減少多項式的維度。假設 f(x) = 1744 * x^{185423},加入第二變數 y,使 y = x^{1000},所以多項式可改寫為 g(x, y) = 1744*x^{423}*y^{185}。藉由這樣的方式,從本來10萬的維度變成1千,藉由這種技巧大幅降低多項式的維度。在 FRI 目前的實做,是將維度對半降低 y = x²(f(x) = g(x, x²))。
此外,還有另一個技巧,將一個多項式拆成兩個較小的多項式,把偶數次方跟奇數次方拆開,如下:
f(x)= g(x²) + xh(x²)
假如:
f(x) = a0 + a1x + a2x² + a3x³ + a4x⁴ + a5x⁵
g(x²) = a0 + a2x² + a4x⁴, (g(x) = a0 + a2x + a4x²)
h(x²) = a1x + a3x² + a5x⁴, (h(x) = a1 + a3x + a5x² )
藉由這兩個方法,可以將高維度的多項式拆解,重複地將維度對半再對半,以此類推到常數項。而 FRI 協議在流程上包含兩階段 — 「提交」跟「查詢」。
提交階段:提交階段就如同上述過程,將多項式拆解後,由驗證者提供一亂數,組成新的多項式,再繼續對多項式拆解,一直重複。
f(x) = f0(x) = g0(x²) + x*h0(x²)
==> f1(x) = g0(x) + α0*h0(x), ← α0(驗證者提供)
==> f2(x) = g1(x) + α1*h1(x), ← α1(驗證者提供)
==> . . .
查詢階段:這個階段要驗證證明者所提交的多項式 f0(x), f1(x), f2(x), … 是否正確,這邊運用一個技巧,帶入任意數 z 及 -z(這代表在選域的時候,需滿足 L²= {x²:x ∊ L},這邊不多提)。所以可以得
f0(z) = g0(z²) + z*h0(z²)
f0(-z) = g0(z²) -z*h0(z²)
藉由兩者相加、相減,及可得g0(z²)、h0(z²),則可以計算出f1(z²),再推導出f1(x),以此類推驗證證明者傳來的多項式。
Interactive Oracle Proofs (IOPs)
藉由FRI(RS糾刪碼、IOPs),將驗證次數由數百萬降至20–30次(log2(d)),達到了簡潔地驗證。不過,我們解決了複雜度,但還有互動性!
* 與SNARK比較 :SNARK在驗證方面利用了QAP跟Pinocchio協定。
非互動性
藉由 Micali 建構(Micali construction)這個概念來解釋如何達到非互動的驗證。Micali 建構包括兩部分,PCPs(Probabilistically checkable proof)跟雜湊函數。PCPs 這是一個隨機抽樣檢查的證明系統。簡單來說,證明者產出一個大資料量的證明(long proof),經由隨機抽樣來驗證這個大資料量的證明。過程大約是這樣,證明者產出證明𝚿,而驗證者隨機確認 n 個點是否正確。
在STARK,我們希望達到:1.小的證明量,2.非互動。隨機抽樣可以讓達到小的證明量,那互動性呢? 想法很簡單,就是預先抽樣,把原本 PCPs 要做的事先做完,然後產出只有原本證明 𝚿 抽樣出的幾個區塊當作證明。但想也知道,一定不會是由證明者抽樣,因為這樣就可以作假。這裡是使用 Fiat-Shamir Heuristic 來作預先取樣。
首先,先把證明 𝚿組成 merkle tree,接著把 merkle root 做雜湊可得到一亂數 𝛒,而 𝛒 就是取樣的索引值。將利用𝛒取出來的區塊證明、區塊證明的 merkle tree 路徑跟 merkle root, 組一起,即為STARK 證明 𝛑。
到目前,只使用雜湊函數這個密碼學的輕量演算法。而雜湊函數的選擇是這個證明系統唯一的全域參數(大家都需要知道的),不像是 SNARK 有 KCA 使用的(α, β, 𝛾)等全域的秘密參數,再藉由 HH(同態隱藏)隱藏這些資訊來產生 CRS。因為證明的驗證是靠公開的雜湊函數,並不需要預先產生的秘密,因此 STARK 可以達到透明性,也不用可信任的設置。
接著,將FRI中需要互動的部分(驗證者提供 α 變數),使用上述的 PCP + Fiat-Shamir Heuristic, 即可達到非互動性。
* 與SNARK比較: SANRK 的非互動性是將所需的全域參數放到CRS中,因為全域參數是公開的,所以CRS裡的值使用了 HH 做隱藏。
MIMC
大部分證明系統,會使用算數電路來實作,此時,電路的複雜程度就關係到證明產生的速度。 STARK 的雜湊函數選用了電路複雜度較簡單的 MIMC,計算過程如下:
https://vitalik.ca/general/2018/07/21/starks_part_3.html
這樣的計算有另一個特性,就是無法平行運算,但卻又很好驗證,因此也很適合 VDF 的運算。Vitalik有一個使用 MIMIC 作為 VDF 的提案。
ps. 反向運算比正向慢百倍,所以會是反向計算,正向驗證
從上面的解釋,可以理解為什麼 STARK 不需要可信任設置,至於為什麼能抗量子?因為 SNARK 中使用了 HH 來隱藏秘密,而 HH 是依靠橢圓曲線的特性,但橢圓曲線沒有抗量子的特性(也就是可以從公鑰回推私鑰)。而STARK在整個過程中只使用了雜湊函數,而目前還沒有有效的演算法能破解雜湊函數,因此可以抵抗抗量子攻擊。
有錯誤或是不同看法,歡迎指教
參考:
StarkDEX Deep Dive: the STARK Core Engine
STARK 系列文:
STARK Math: The Journey Begins
Arithmetization I
Arithmetization II
Low Degree Testing
A Framework for Efficient STARKs
Vitalik 系列文:
STARKs, Part I: Proofs with Polynomials
STARKs, Part II: Thank Goodness It’s FRI-day
STARKs, Part 3: Into the Weeds
ZK-STARKs — Create Verifiable Trust, even against Quantum Computers
https://ethereum.stackexchange.com/questions/59145/zk-snarks-vs-zk-starks-vs-bulletproofs-updated
Originally published at http://kimiwublog.blogspot.com on November 12, 2019.
瞭解神秘的 ZK-STARKs was originally published in Taipei Ethereum Meetup on Medium, where people are continuing the conversation by highlighting and responding to this story.
👏 歡迎轉載分享鼓掌
變數常數運算子 在 COMPOTECHAsia電子與電腦 - 陸克文化 Facebook 的精選貼文
#物聯網IoT #汽車電子 #ISO26262 #電子設計自動化EDA #晶片變異OCV #人工智慧AI #機器學習MachineLearning #FPGA #視覺運算 #卷積神經網路CNN #雷達/光達 #點雲PointCloud #高效能運算HPC #系統單晶片SoC #系統級封裝SiP
【AI 不該閉門造車或犧牲血汗勞力換取!】
半導體製程微縮,讓晶片實體化工作更須謹慎以對。28 nm 之前只要留意間距空隙,基本上即大勢底定;但進入 28 nm 以下,金屬線的粗細、長短皆可能為製程憑添變數——在此之前,晶片繞線的規則相對單純;但越往先進製程發展,形態越多變且容易重疊。到了 10 nm 以下,若金屬線徑未隨著電晶體變小,晶片尺寸仍無法有效縮減;欲降低 CPU 功耗,也無法再透過新的光刻 (lithography) 材料和架構達成目的,須借助設計與系統級技術共同優化。
以常數作為額定值降低系數 (derating factor) 推估「晶片變異」(OCV) 的建模方式不再適用。當變異來源擴大,勢必得輔以統計與機率概念,才能直搗黃龍、加速實作工程。為弄清層層疊疊、錯綜複雜的脈絡關係,結合「機器學習」(Machine Learning) 的電子設計自動化 (EDA) 工具可從龐大的訓練組合中萃取設計資料精華,減少試誤徒勞及來回修正。此外,「異質晶片堆疊」的互連 (interconnect) 功耗、各層執行速度、立體封裝乃至時脈架構,皆與高效能混合訊號設計密不可分。
使用者能有多大耐心操作智能裝置?開發者又有多少時間能搶搭商機?物聯網 (IoT) 不是只有連上網路就好,重要的是如何收集有用的數據,並培育正向人工智慧 (AI) 作為助力。藉由將 AI 概念導入設計工具可加速「核心引擎」,盡速以數學推演收斂適用的 IP 集合,並經由模擬檢驗是否符合預期?還有助於將引擎中的 ASIC 模擬結果與 FPGA 編程環境無縫接軌,既可解決 FPGA 承載有限的問題,又能讓軟體工程師同步編譯,不須挨到晶片就緒才開始動作。
進行情境模擬時,也不須逐一打開描述文檔、餵入資料才能展示影像成果,可聰明地自動成像 (Render),更具「即視感」、方便即時修正設計。因此,EDA 須朝向快捷、智慧、全流程演進——平行運算提升處理速度、精煉經驗增強預知能力以及統一引擎貫穿設計流程,已是必然走向。可惜,就 EDA 廠商觀察,台灣廠商雖勤於模擬工作,卻相對忽略「驗證」環節,棋差一著的後果,換來的是時間、金錢上的滿盤皆輸……。
延伸閱讀:
《IoT 下一站哩程:萃取大數據 ==> 培育人工智慧》
http://compotechasia.com/a/shi__shang_/2017/0915/36703.html
(點擊內文標題即可閱讀全文)
#益華電腦Cadence #Tensilica #TÜV SÜD #日月光 #鴻海 #鴻佰科技
★★【智慧應用開發論壇】(FB 不公開社團:https://www.facebook.com/groups/smart.application/) 誠邀各界擁有工程專業或實作經驗的好手參與討論,採「實名制」入社。申請加入前請至 https://goo.gl/forms/829J9rWjR3lVJ67S2 填寫基本資料,以利規劃議題方向;未留資料者恕不受理。★★
變數常數運算子 在 吳老師教學部落格 Youtube 的精選貼文
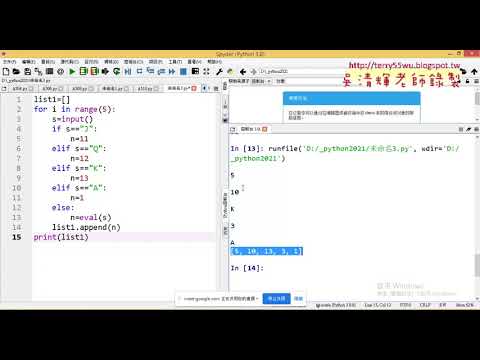
Python基礎程式語言應用證照班第10次上課
01_重點回顧與證照508最大公因數
02_證照508最大公因數解答
03_證照510費氏數列題目說明
04_證照510費氏數列無函式解答
05_證照510費氏數列加上函式解答
06_證照602撲克牌總和解答一
07_證照602撲克牌總和解答二改用串列
08_證照604眾數建立串列與新增
09_證照604眾數用COUNT計算次數
完整教學
http://goo.gl/aQTMFS
吳老師教學論壇
http://www.tqc.idv.tw/
教學論壇(之後課程會放論壇上課學員請自行加入):
https://groups.google.com/g/tcfst_python_2021_2
證照基礎程式語言 (Python 3)證照
Python 第1類:基本程式設計
技能內容:變數與常數、指定敘述、標準輸入輸出、運算式、算術運算子、數學函式的應用、格式化的輸出Python 第2類:選擇敘述
技能內容:if、if...else、if…elifPython 第3類:迴圈敘述
技能內容:while、for…inPython 第4類:進階控制流程
技能內容:常用的控制結構、條件判斷、迴圈Python 第5類:函式(Function)
技能內容:函式使用、傳遞參數、回傳資料、內建函式、區域變數與全域變數
上課用書:
Python 3.x 程式語言特訓教材(第二版)
作者: 蔡明志, 財團法人中華民國電腦技能基金會
出版社:全華
出版日期:2018/12/20
定價:490元
吳老師 110/9/14
EXCEL,VBA,Python,自強工業基金會,EXCEL,VBA,函數,程式設計,線上教學,PYTHON安裝環境
變數常數運算子 在 吳老師教學部落格 Youtube 的最佳貼文
Python基礎程式語言應用證照班第10次上課
01_重點回顧與證照508最大公因數
02_證照508最大公因數解答
03_證照510費氏數列題目說明
04_證照510費氏數列無函式解答
05_證照510費氏數列加上函式解答
06_證照602撲克牌總和解答一
07_證照602撲克牌總和解答二改用串列
08_證照604眾數建立串列與新增
09_證照604眾數用COUNT計算次數
完整教學
http://goo.gl/aQTMFS
吳老師教學論壇
http://www.tqc.idv.tw/
教學論壇(之後課程會放論壇上課學員請自行加入):
https://groups.google.com/g/tcfst_python_2021_2
證照基礎程式語言 (Python 3)證照
Python 第1類:基本程式設計
技能內容:變數與常數、指定敘述、標準輸入輸出、運算式、算術運算子、數學函式的應用、格式化的輸出Python 第2類:選擇敘述
技能內容:if、if...else、if…elifPython 第3類:迴圈敘述
技能內容:while、for…inPython 第4類:進階控制流程
技能內容:常用的控制結構、條件判斷、迴圈Python 第5類:函式(Function)
技能內容:函式使用、傳遞參數、回傳資料、內建函式、區域變數與全域變數
上課用書:
Python 3.x 程式語言特訓教材(第二版)
作者: 蔡明志, 財團法人中華民國電腦技能基金會
出版社:全華
出版日期:2018/12/20
定價:490元
吳老師 110/9/14
EXCEL,VBA,Python,自強工業基金會,EXCEL,VBA,函數,程式設計,線上教學,PYTHON安裝環境
變數常數運算子 在 吳老師教學部落格 Youtube 的精選貼文
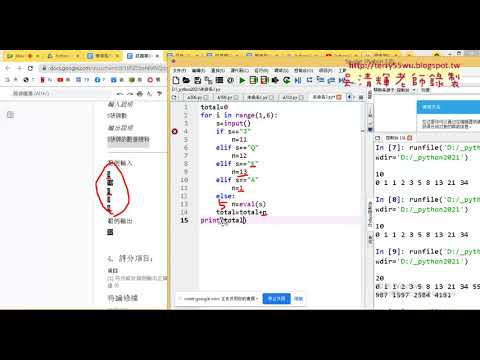
Python基礎程式語言應用證照班第10次上課
01_重點回顧與證照508最大公因數
02_證照508最大公因數解答
03_證照510費氏數列題目說明
04_證照510費氏數列無函式解答
05_證照510費氏數列加上函式解答
06_證照602撲克牌總和解答一
07_證照602撲克牌總和解答二改用串列
08_證照604眾數建立串列與新增
09_證照604眾數用COUNT計算次數
完整教學
http://goo.gl/aQTMFS
吳老師教學論壇
http://www.tqc.idv.tw/
教學論壇(之後課程會放論壇上課學員請自行加入):
https://groups.google.com/g/tcfst_python_2021_2
證照基礎程式語言 (Python 3)證照
Python 第1類:基本程式設計
技能內容:變數與常數、指定敘述、標準輸入輸出、運算式、算術運算子、數學函式的應用、格式化的輸出Python 第2類:選擇敘述
技能內容:if、if...else、if…elifPython 第3類:迴圈敘述
技能內容:while、for…inPython 第4類:進階控制流程
技能內容:常用的控制結構、條件判斷、迴圈Python 第5類:函式(Function)
技能內容:函式使用、傳遞參數、回傳資料、內建函式、區域變數與全域變數
上課用書:
Python 3.x 程式語言特訓教材(第二版)
作者: 蔡明志, 財團法人中華民國電腦技能基金會
出版社:全華
出版日期:2018/12/20
定價:490元
吳老師 110/9/14
EXCEL,VBA,Python,自強工業基金會,EXCEL,VBA,函數,程式設計,線上教學,PYTHON安裝環境





